QAOA M$\kappa$CS#

The Max-$\kappa$-Colorable Subgraph problem and its QAOA implementation is discussed in plenty of detail in the Max-$\kappa$-Colorable Subgraph tutorial. All the necessary ingredients and required steps to run QAOA are elaborated on in an easy to grasp manner.

Here, we provide a condensed implementation of QAOA for M$\kappa$CS using all of the predefined functions.

Problem description#

Given a Graph $G = (V,E)$ and $\kappa$ colors, maximize the size (number of edges) of a properly colored subgraph.

Cost operator#

create_coloring_operator(G)[source]#

Generates the cost operator for an instance of the coloring problem for a given graph G.

The coloring operator and applies a phase if two neighboring nodes in the graph have the same color.

Parameters:

Gnx.Graph: The graph to color.

Returns:

cost_operatorfunction: A function receiving a QuantumVariable and a real parameter $\gamma$. This function performs the application of the cost operator.

Classical cost function#

create_coloring_cl_cost_function(G)[source]#

Creates the classical cost function for an instance of the coloring problem for a given graph G.

Parameters:

Gnx.Graph: The graph to color.

Returns:

cl_cost_functionfunction: The classical cost function for the problem instance, which takes a dictionary of measurement results as input.

Coloring problem#

graph_coloring_problem(G)[source]#

Creates a QAOA problem instance with appropriate phase separator, mixer, and classical cost function.

Parameters:

Gnx.Graph: The graph to color.

Returns:

QAOAProblemfunction: A QAOA problem instance for graph coloring for a given graph G.

Example implementation#

from qrisp import QuantumArray
from qrisp.qaoa import QAOAProblem, RX_mixer, apply_XY_mixer, QuantumColor, create_coloring_cl_cost_function, create_coloring_operator
import networkx as nx
import random
from operator import itemgetter

G = nx.Graph()
G.add_edges_from([[0,1],[0,4],[1,2],[1,3],[1,4],[2,3],[3,4]])
color_list = ["red", "blue", "yellow", "green"]

qarg = QuantumArray(qtype = QuantumColor(color_list, one_hot_enc=True), shape = G.number_of_nodes())
#qarg = QuantumArray(qtype = QuantumColor(color_list, one_hot_enc=False), shape = G.number_of_nodes()) # use one_hot_enc=False for binary encoding

qaoa_coloring = QAOAProblem(cost_operator=create_coloring_operator(G),
                        mixer=apply_XY_mixer, # use RX_mixer for binary encoding
                        cl_cost_function=create_coloring_cl_cost_function(G))

init_state = [random.choice(color_list) for _ in range(len(G))]
qaoa_coloring.set_init_function(lambda x : x.encode(init_state))

result = qaoa_coloring.run(qarg=qarg, depth=3, max_iter=50)

That’s it! In the following, we print the 5 most likely solutions together with their cost values.

cl_cost =create_coloring_cl_cost_function(G)

print("5 most likely solutions")
max_five = sorted(result.items(), key=lambda item: item[1], reverse=True)[:5]
for res, prob in max_five:
    print(res, prob, cl_cost({res : 1}))

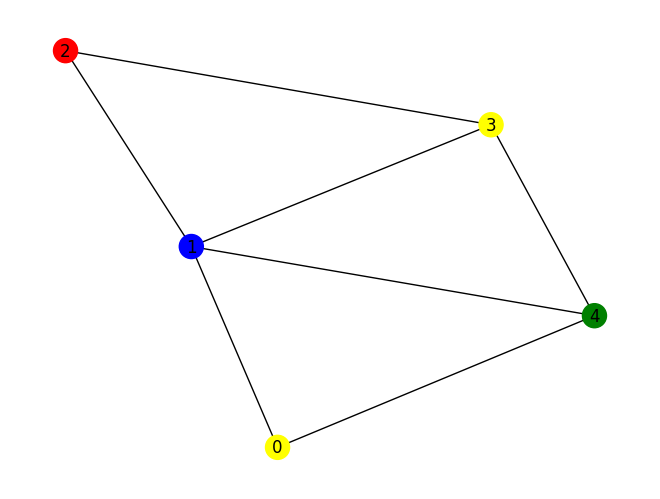
Finally, we visualize the most likely solution.

best_of_five = min([(cl_cost({item[0]:1}),item[0]) for item in max_five], key=itemgetter(0))[1]
nx.draw(G, with_labels=True,
        node_color=[best_of_five[node] for node in G.nodes()])