QAOA MaxClique#

Problem description#

Given a Graph $G = (V, E)$ find a maximum clique, i.e., a subset of vertices $V^{'} \subset V$ such that all pairs of vertices are adjacent in the graph $G$ . Following the work of Hadfield et al., the MaxClique problem is solved by solving the MaxIndepSet problem on the complement graph.

Classical cost function#

create_max_clique_cl_cost_function(G)[source]#

Creates the classical cost function for an instance of the maximum clique problem for a given graph G.

Parameters:

Gnx.Graph: The Graph for the problem instance.

Returns:

cl_cost_functionfunction: The classical cost function for the problem instance, which takes a dictionary of measurement results as input.

MaxClique problem#

max_clique_problem(G)[source]#

Creates a QAOA problem instance with appropriate phase separator, mixer, and classical cost function.

Parameters:

Gnx.Graph: The graph for the problem instance.

Returns:

QAOAProblem: A QAOA problem instance for MaxClique for a given graph G.

Example implementation#

from qrisp import QuantumVariable
from qrisp.qaoa import QAOAProblem, RZ_mixer, create_max_indep_set_cl_cost_function, create_max_indep_set_mixer, max_indep_set_init_function
import networkx as nx

G = nx.erdos_renyi_graph(9, 0.7, seed =  133)
G_complement = nx.complement(G)
qarg = QuantumVariable(G.number_of_nodes())

qaoa_max_clique = QAOAProblem(cost_operator=RZ_mixer,
                                mixer=create_max_indep_set_mixer(G_complement),
                                cl_cost_function=create_max_indep_set_cl_cost_function(G_complement),
                                init_function=max_indep_set_init_function)
results = qaoa_max_clique.run(qarg=qarg, depth=5)

That’s it! In the following, we print the 5 most likely solutions together with their cost values.

cl_cost = create_max_indep_set_cl_cost_function(G_complement)

print("5 most likely solutions")
max_five = sorted(results.items(), key=lambda item: item[1], reverse=True)[:5]
for res, prob in max_five:
    print([index for index, value in enumerate(res) if value == '1'], prob, cl_cost({res : 1}))

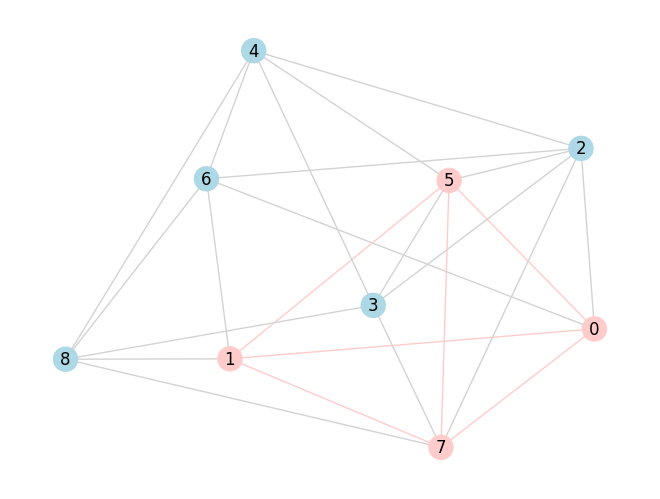
Finally, we visualize the most likely solution.

most_likely = [index for index, value in enumerate(max_five[0][0]) if value == '1']
nx.draw(G, with_labels = True,
        node_color=['#FFCCCB' if node in most_likely else '#ADD8E6' for node in G.nodes()],
        edge_color=['#FFCCCB' if edge[0] in most_likely and edge[1] in most_likely else '#D3D3D3' for edge in G.edges()])