qrisp.vqe.VQEProblem.benchmark#

VQEProblem.benchmark(qarg, depth_range, shot_range, iter_range, optimal_energy, repetitions=1, mes_kwargs={}, init_type='random')[source]#

This method enables convenient data collection regarding performance of the implementation.

Parameters:

qargQuantumVariable or QuantumArray: The quantum argument the benchmark is executed on. Compare to the .run method.
depth_rangelist[int]: A list of integers indicating, which depth parameters should be explored. Depth means the amount of VQE layers.
shot_rangelist[int]: A list of integers indicating, which shots parameters should be explored. Shots means the amount of repetitions, the backend performs per iteration and per measurement setting.
iter_rangelist[int]: A list of integers indicating, what iterations parameter should be explored. Iterations means the amount of backend calls, the optimizer is allowed to do.
optimal_energy: float: The exact ground state energy of the problem Hamiltonian.
repetitionsint, optional: The amount of repetitions, each parameter constellation should go though. Can be used to get a better statistical significance. The default is 1.
mes_kwargsdict, optional: The keyword arguments, that are used for the qarg.get_spin_measurement. The default is {}.
init_typestring, optional: Specifies the way the initial optimization parameters are chosen. Available is random. The default is random: Parameters are initialized uniformly at random in the interval \([0,\pi/2)]\).

Returns:

VQEBenchmark: The results of the benchmark.

Examples

We create a Heisenberg problem instance and benchmark several parameters:

from networkx import Graph

G =Graph()
G.add_edges_from([(0,1),(1,2),(2,3),(3,4)])
from qrisp.vqe.problems.heisenberg import *

vqe = heisenberg_problem(G,1,0)
H = create_heisenberg_hamiltonian(G,1,0)

benchmark_data = vqe.benchmark(qarg = QuantumVariable(5),
                    depth_range = [1,2,3],
                    shot_range = [5000,10000],
                    iter_range = [25,50],
                    optimal_energy = H.ground_state_energy(),
                    repetitions = 2
                    )

We can investigate the data by calling visualize:

benchmark_data.visualize()

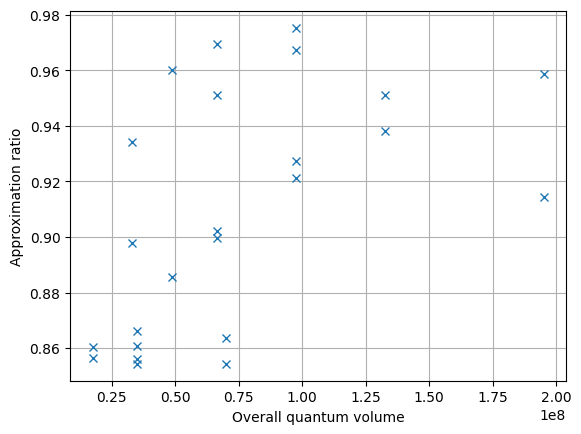
../../../../_images/vqe_benchmark_plot.png

The VQEBenchmark class contains a variety of methods to help you drawing conclusions from the collected data. Make sure to check them out!