VQE Heisenberg model#

Heisenberg problem#

heisenberg_problem(G, J, B, ansatz_type='per hamiltonian')[source]#

Creates a VQE problem instance for an isotropic Heisenberg model defined by a graph $G = (V, E)$ , the coupling constant $J > 0$ (antiferromagnetic), and the magnetic field strength $B$ . The model Hamiltonian is given by:

H = J \sum_{(i, j) \in E} (X_{i} X_{j} + Y_{i} Y_{j} + Z_{i} Z_{j}) + B \sum_{i \in V} Z_{i}

Each Hamiltonian $H_{i, j} = X_{i} X_{j} + Y_{i} Y_{j} + Z_{i} Z_{j}$ has three eigenvectors for eigenvalue $+ 1$ (triplet states):

$| 00 ⟩$
$| 11 ⟩$
$\frac{1}{\sqrt{2}} (| 10 ⟩ + | 01 ⟩)$

and one eigenvector for eigenvalue $- 3$ (singlet state):

$\frac{1}{\sqrt{2}} (| 10 ⟩ - | 01 ⟩)$

For the problem specific VQE ansatz, we choose a Hamiltonian Variational Ansatz as proposed here. This ansatz is inspired by the adiabatic theorem of quantum mechanics: A system is prepared in the ground state of an initial Hamiltonian $H_{0}$ and then slowly evolved under a time-dependet Hamiltoniam $H (t)$ . Here, we set

H (t) = (1 - \frac{t}{T}) H_{0} + \frac{t}{T} H

where

H_{0} = \sum_{(i, j) \in M} (X_{i} X_{j} + Y_{i} Y_{j} + Z_{i} Z_{j})

for a maximal matching $M \subset E$ of the graph $G$ .

For $J > 0$ the ground state of the initial Hamiltonian $H_{0}$ is given by a tensor product of singlet states corresponding to the maximal matching $M$ .

The time evolution of $H (t)$ is approximately implemented by trotterization, i.e., alternatingly applying $e^{- i H_{0} Δ t}$ and $e^{- i H Δ t}$ , and if necessary trotterizing $e^{- i H Δ t}$ .

In the scope of VQE, the short evolution times $Δ t$ are replaced by parameters $θ_{i}$ which are then optimized. This yields the following unitary ansatz with $p$ layers:

U (θ) = \prod_{l = 1}^{p} e^{- i θ_{l, 0} H_{0}} e^{- i θ_{l, 1} H}

The unitary $e^{- i θ H}$ trotterized by:

U_{H} (θ) = e^{- i θ H_{B}} \prod_{k = 1}^{q} \prod_{(i, j) \in E_{k}} e^{- i θ H_{i j}}

where $E_{1}, \dots, E_{q}$ is an edge coloring of the graph $G$ , and $H_{B}$ is the magnetic field Hamiltonian. Then all unitaries $e^{- i θ H_{i j}}$ for $(i, j) \in E_{k}$ commute. For implementing such unitaries, note that each two-qubit Heisenberg interaction unitary

\begin{array}{r} Heis (θ) \equiv e^{- i θ / 4} e^{- i θ H_{i j}} = (\begin{array}{c} e^{- i θ / 2} & 0 & 0 & 0 \\ 0 & \cos (θ / 2) & - i \sin (θ / 2) & 0 \\ 0 & - i \sin (θ / 2) & \cos (θ / 2) & 0 \\ 0 & 0 & 0 & e^{- i θ / 2} \end{array}) \end{array}

becomes diagonal in Bell basis, i.e., $e^{- i θ / 2} diag (1, 1, 1, e^{i θ})$ .

This ansatz can be further generalized by introducing parameters

per edge color (one parameter for each color)
per edge (one parameter for each edge)

in the unitary $U_{H} (θ)$ .

Parameters:

Gnx.Graph: The graph defining the lattice.
Jfloat: The positive coupling constant.
Bfloat: fhe magnetic field strength.
ansatz_typestring, optional: Specifies the Hamiltonian Variational Ansatz. Available are per hamiltonian, per edge color, per edge. The default is per hamiltonian.

Returns:

VQEProblem: VQE problem instance for a specific isotropic Heisenberg model.

Examples

import networkx as nx
import matplotlib.pyplot as plt

# Create a graph
G = nx.Graph()
G.add_edges_from([(0,1),(1,2),(2,3),(0,3)])

# Draw the graph with labels
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_size=700, node_color='lightblue')
nx.draw_networkx_labels(G, pos)
plt.show()

../../../../_images/heisenberg_lattice.png

from qrisp import QuantumVariable
from qrisp.vqe.problems.heisenberg import *

vqe = heisenberg_problem(G,1,1)
vqe.set_callback()
energy = vqe.run(QuantumVariable(G.number_of_nodes()),depth=2,max_iter=50)
print(energy)
# Yields -8.0

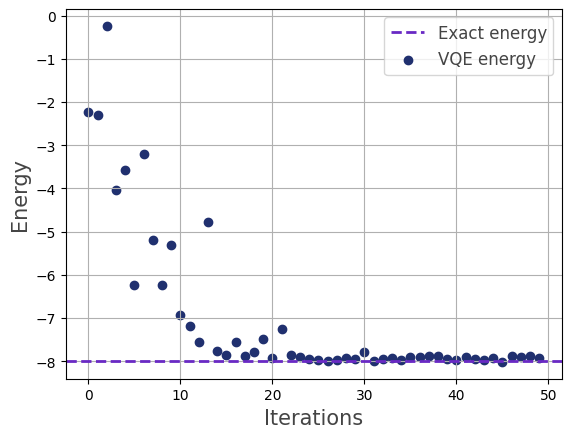
We visualize the optimization process:

>>> vqe.visualize_energy(exact=True)

../../../../_images/heisenberg_energy.png

Hamiltonian#

create_heisenberg_hamiltonian(G, J, B)[source]#

This method creates the Hamiltonian for the Heisenberg model.

Parameters:

Gnx.Graph: The graph defining the lattice.
Jfloat: The positive coupling constant.
Bfloat: The magnetic field strength.

Returns:

HQubitOperator: The quantum Hamiltonian.

Ansatz#

create_heisenberg_ansatz(G, J, B, M, C, ansatz_type='per hamiltonian')[source]#

This method creates a function for applying one layer of the ansatz.

Parameters:

Gnx.Graph: The graph defining the lattice.
Jfloat: The positive coupling constant.
Bfloat: The magnetic field strength.
Mlist: A list of edges corresponding to a maximal matching of G.
Clist: An edge coloring of the graph G given by a list of lists of edges.
ansatz_typestring, optional: Specifies the Hamiltonian Variational Ansatz. Available are per hamiltonian, per edge color, per edge. The default is per hamiltonian.

Returns:

ansatzfunction: A function that can be applied to a QuantumVariable and a list of parameters.

create_heisenberg_init_function(M)[source]#

Creates the function that, when applied to a QuantumVariable, initializes a tensor product of singlet sates corresponding to a given matching.

Parameters:

Mlist: A list of edges corresponding to a maximal matching of G.

Returns:

init_functionfunction: A function that can be applied to a QuantumVariable.